一直都在说高中数学难,大家可能觉得我在渲染焦虑。
所以想来想去还是拿事实说话,也帮助大家有一个直观的认识。比如你是一名家长,刚训斥完孩子不够努力,谁知转眼间发现自己穿越回青葱岁月,是一名高中二年级的学生,你现在开始了一轮复习
。
咦,为什么我当初都是高三才复习,现在怎么高二期中考试之后就要复习了?你有些疑问,但无所谓了,你要逆天改命!你抱着要把高中数学的犄角旮旯所有细节都一网打尽的决心,学到了函数的单调性和最值。你打开学校配发的教辅,发现只有讲义只有寥寥三面,呃,两面半。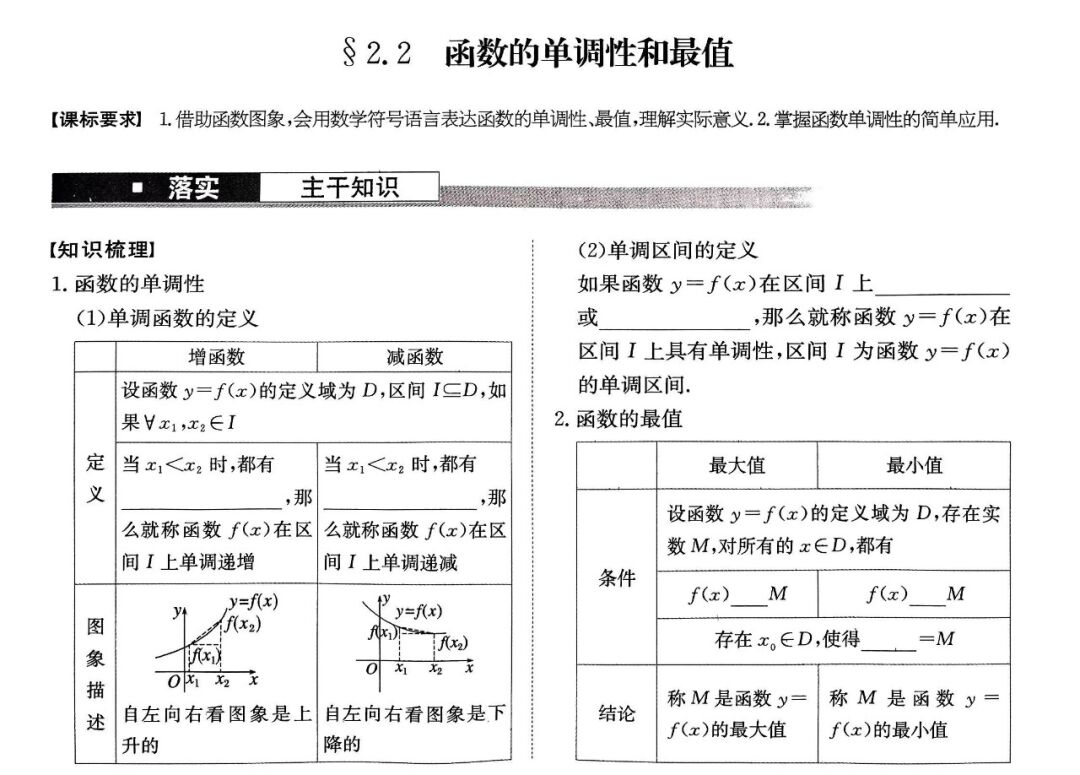

 这还不轻松拿捏?你踌躇满志的想。“且慢”,你的数学老师拦着你,“我先问你一些问题,看你掌握的怎么样?”
这还不轻松拿捏?你踌躇满志的想。“且慢”,你的数学老师拦着你,“我先问你一些问题,看你掌握的怎么样?”

“你看这个命题点1,是函数单调性的判断,那么请你给我讲一讲,函数单调性的判断与证明有哪些方法?”
这有何难?
你表示这根本难不倒你。
“首先是定义法,其次……”
“且慢,定义法证明单调性需要注意什么?”
“区间吧,要考虑单调性所在的区间;
还有任意性,一定要写任意的两个自变量;
然后就是作差,判断差和0的大小关系。”
“那咋判断差和0的大小关系?”
“呃,需要通分,然后因式分解,将结果转化成若干项相乘、或者相除的形式,这样比较好判断!”
你一次性说的有点多,忍不住喘了口气。
“bingo!那么只能作差吗?”
“也…..不是吧,也可以做商吧?”
“哦?那做商有什么限制条件呢?”
“做商……一般要保证两项符号一致吧,同正或者同负。”
“那比如说两项同正,商大于1,分子大还是分母大,两项同负又如何呢?”
“两项同正商大于1,分子比分母大;两项同负商大于1,分子比分母小。”
“好的,你继续,还有什么判断单调性的方法?”
“还可以利用单调函数相加减的规律来判断。”
“什么规律?”
“增+增=增,减+减=减……”
“就只有这?”老师有些失望。
“啊?”你委婉的表示想不起来了。
“增-减=增,减-增=减,正数×增(减)=增(减),负数×增(减)=减(增),如果函数值域是大于0或者小于0,增的倒数是减,减的倒数是增,平方开方不影响单调性……”老师一口气说的口干舌燥,你赶紧递上一杯水。
“记住了吗?”
“记住了,记住了。”
“哦,那这些一定成立吗?”老师意味深长的问。
“啊不不不,你连忙否认,要是多个部分的话,要在公共定义域内讨论。”
老师非常满意,“说的很好,这样的话就需要对各种函数的单调性有认识对吧?”
“……对。”你有一种不祥的预感。
“那就把所有你知道的函数的单调性给我列一遍吧!”老师愉快的说道。
你默默的表示各位读者朋友我实在不想打字了,我小红书找个图您各位脑补下我回答的过程吧。
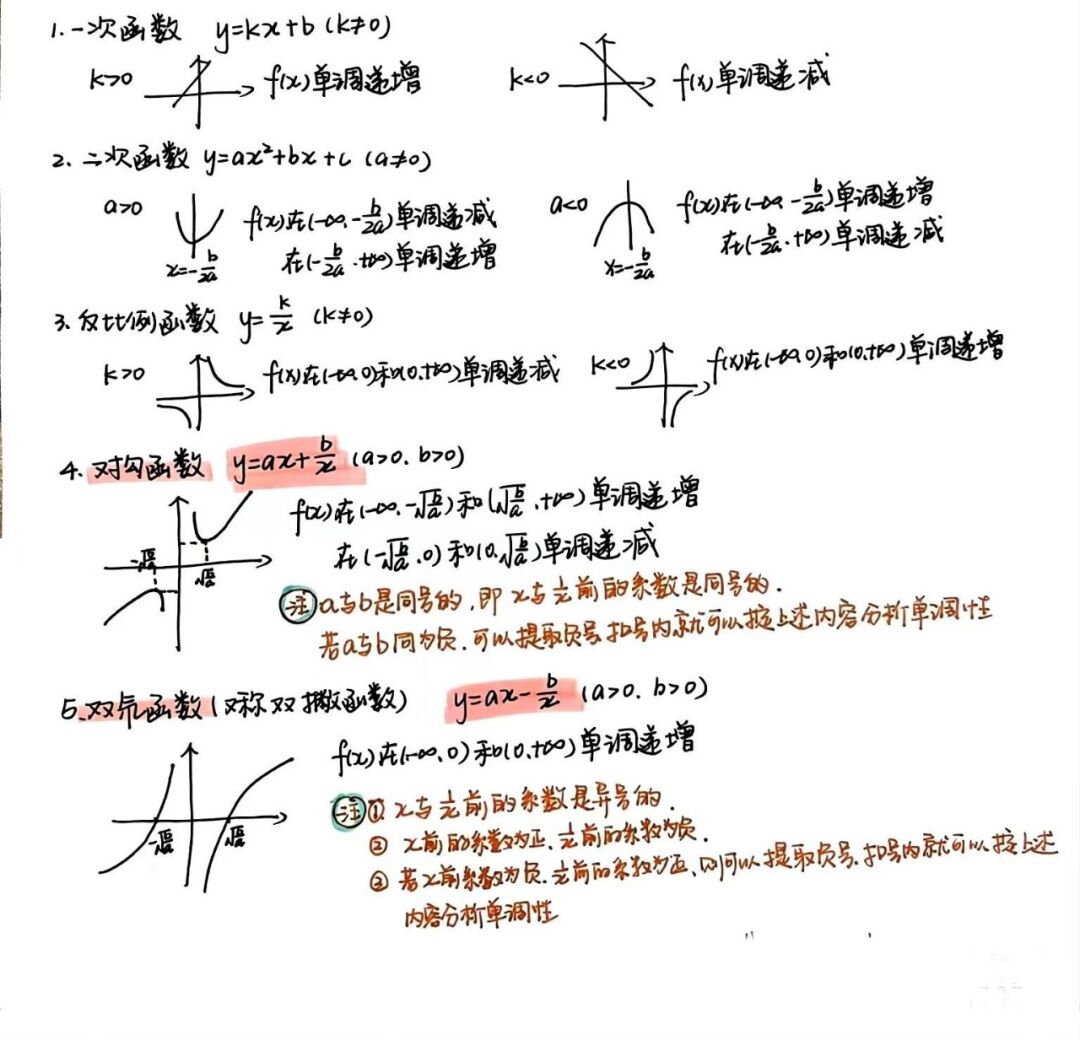
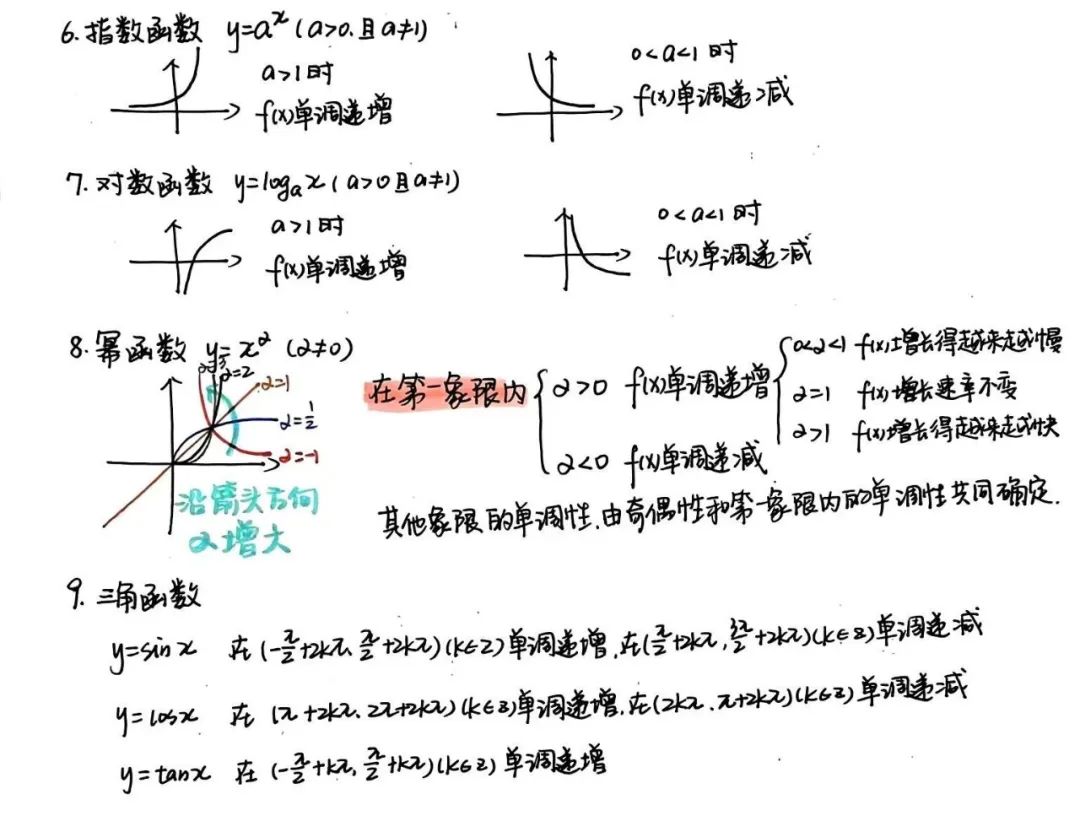 以上内容来自于小红书用户兰奇你默默的感谢了这位小红书用户,把其中的内容给老师讲了一遍。老师看了一遍,表示满意。就在你以为到此结束时,他老人家又发话了。“掌握的不错,可是考试的时候不会这样直接考啊,一般会加一些变化,你知道有哪些变化?”“呃,有时候会结合图像变换…..”说到这里你就有一个不祥的预感。“哦,图像变换都有哪些啊?”你在心里默默的和老师一起把问题说出来。认命的叹了口气,你又打开小红书。你在一个名叫管综数学汪老师的小红书用户那里借了张图,交给了老师。
以上内容来自于小红书用户兰奇你默默的感谢了这位小红书用户,把其中的内容给老师讲了一遍。老师看了一遍,表示满意。就在你以为到此结束时,他老人家又发话了。“掌握的不错,可是考试的时候不会这样直接考啊,一般会加一些变化,你知道有哪些变化?”“呃,有时候会结合图像变换…..”说到这里你就有一个不祥的预感。“哦,图像变换都有哪些啊?”你在心里默默的和老师一起把问题说出来。认命的叹了口气,你又打开小红书。你在一个名叫管综数学汪老师的小红书用户那里借了张图,交给了老师。 “不错,不错,基础蛮扎实嘛!今天时间有限,就不考察你做题了,你说说单调性判断还会有什么变化?”
“不错,不错,基础蛮扎实嘛!今天时间有限,就不考察你做题了,你说说单调性判断还会有什么变化?”
“还有复合函数。”你感觉这事完不了了,搞不好今天要交代到这里,开始回忆自己哪里得罪了老师,是给他起外号还是给他自行车放气还是把他标准照p成了谢顶……
“复合函数单调性遵循什么原则啊?”
“同增异减。”
“很好,看来你掌握的真不错,那我考考你,能不能证明一下?”
你飞速的扒拉了一下小红书,咦,这个竟然没有?!
没办法你只有百度了一下,虽然不太标准,但总是有了。

你把过程交给老师,常舒了一口气。
却万万没想到,老师又开始继续饶有兴趣的引申了,“我们夸张一点,如果是三层函数,内中外分别是增减增,这个函数单调性是什么样的呢?”
看你有些茫然,他叹了口气,“唉,你们现在这些娃啊,都是读书读傻了,真是不如我刚上班时那一届,你下去想想,啊
。”
你以为他要放过你了,谁知道他又开始问了,“那复合函数常见的有什么类型的呢?
”
“有指数型、对数型、根式型……”
“来,做几个题吧。”数学老师有些得意,“受你的启发,我也开始用小红书了,这些题就是我从一个小红书用户数学大大老师那里找到的,正好你给我做做。”

你欲哭无泪,都是小红书,相煎何太急啊!
好不容易把题目做完,没想到老师又开始追问了,“除了前面所说的,证明、判断单调性还有什么变化呢?”
“还有抽象函数…..”你恨不得把自己的嘴给封上,这张破嘴啊!怎么就不懂韬光养晦呢?
“歪瑞古德!”数学老师很欣慰,“你能想到抽象函数的单调性部分,很不错啊!给老师讲讲,抽象函数怎么证明单调性?”
你默默地打开教辅。

“不错!”老师有些高兴了。
“那还有什么判断单调性的方法吗?”
“还有导数!”你这次也不等老师问了,直接开始扒教辅回答。

“不错,真的不错。”数学老师老怀甚慰。“只有你把这些知识都掌握扎实,才能说把函数单调性判断、证明掌握的差不多。”
“但是”你在心里默念道。“但是”,数学老师果然来了个转折,“但是你也不要骄傲,因为你只是知识掌握的差不多,但是具体到题目上,你掌握的又如何呢?如果题目不会做,那不还是两张皮?”你认命的提前拿出笔和演草纸。“对嘛,咱也不说太多了,一说起来一天都说不完,就导数判断函数单调性,你来做几个题!”数学老师大手一挥,你面前出现了几道题目。“这题目都不算难,你做做,一会儿拿来我看。”
的确也不是太难,你也就做了二十多分钟,把这几道题做完了。
拿给老师一看,都对了!
你想着,这下没啥说的了吧!
总得放我走了吧老师,我何德何能让您给我上一对一,往好处想,一个小时四百我已经赚了四五百块了!
谁知道数学老师意犹未尽,“我再给你找点题,这有些少,你等等啊!”他找了本教辅,扒拉了几道题目。好在你天赋异禀,虽然已经高二了,但是眼睛不近视,瞟到了书的名字《新高掌》。于是你趁老师不备把两道例题的答案给找到了。
至于两道练习题现在就徒呼奈何,就只能等到之后在做了。“额,不错不错。但是吧,还是有些细节没有说到,比如奇偶性和单调性的关系,比如幂函数单调性情况,比如分段函数和单调性……同学,路漫漫其修远兮,还要加油啊!我看你导数判断单调性不是很熟练,这个现在新高考有可能出在解答第一题的,回去后要好好练练啊!不光是导数,上面我们讲到的每个点,都需要练习才够啊!”
数学老师语重心长,面对着唯唯诺诺的你,他问道:
这下,你知道高中数学为什么难了吗?
